3.5 Creating new variables

There are basically two ways to create new variables: we can modify an existing variable (groups or formulas), or we can simulate new values for that variable (random sampling.)

If we have a formula that relates two variables, we could predict one based on the other deterministically.

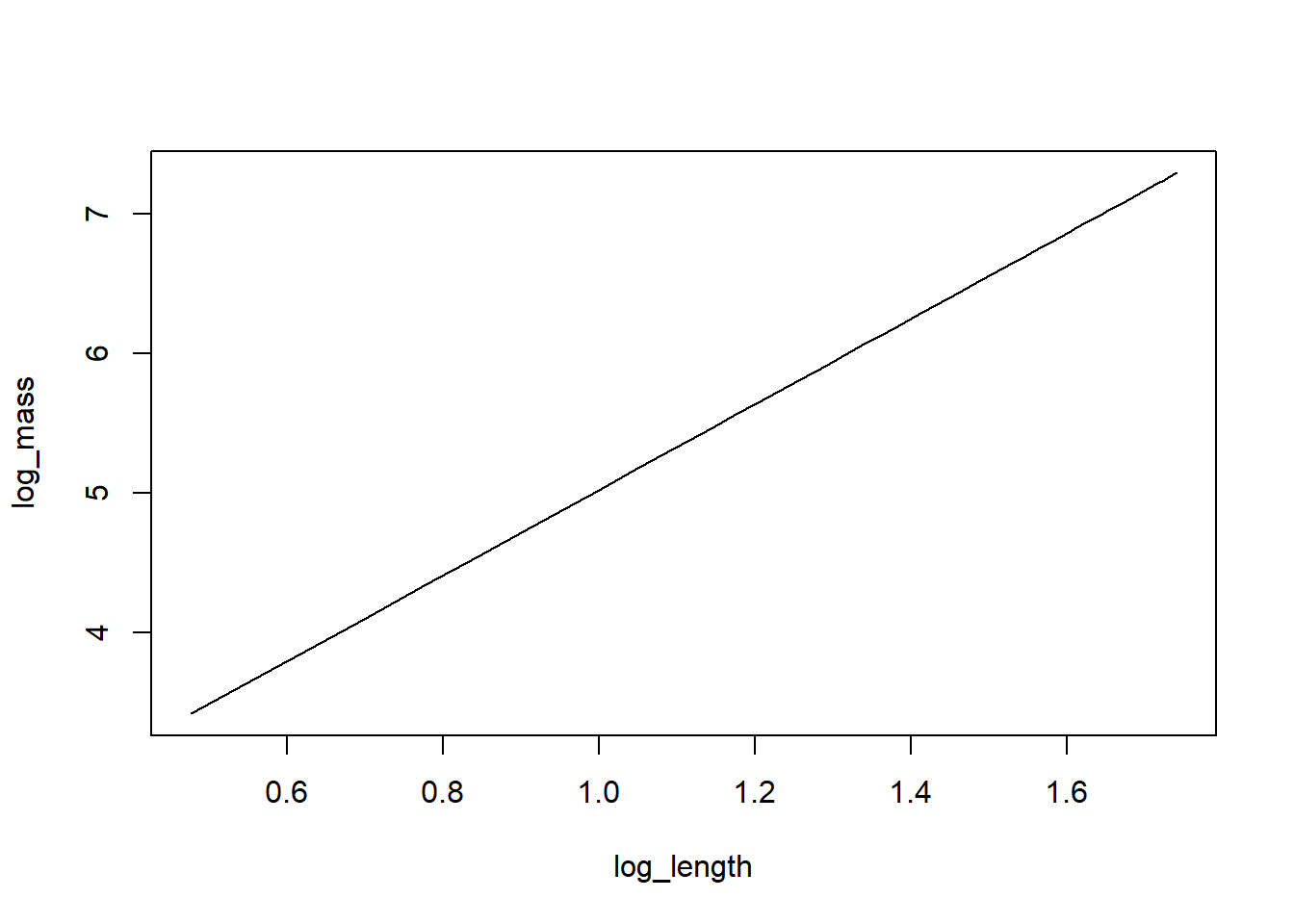
For example, I have fit a length-weight regression to explain the relationship between Length and Mass using the am_shad data we’ve worked with in previous sections.

This relationship looks like your old friend \(y = mx + b\), the equation for a line, but we log10-transform both of the variables before fitting the line (more to come later in the class). Using this relationship, we can predict our independent variable (Mass) from our dependent variable (Length) if we plug in new values for Length and the parameters of the line.

In this case, I know that m = 3.0703621, and b = -1.9535405.

If I plug these numbers in to the equation above, I can predict log10(Mass) for new lengths log10(Length):

\(log_{10}Mass = 3.0703621 \cdot log_{10}Length - 1.9535405\)

In R, this looks like:

# Parameters from length-weight regression
m <- 3.0703621
b <- 1.9535405

# Make a sequence of new lengths based on range in data,
# then take the log of the whole thing all at once.
log_length <- log10( seq(min(am_shad$Length), max(am_shad$Length), 1) )

# Calculate a new thing (log10_mass) using parameters for line
# and sequence of new log10_length.
log_mass <- m * log_length + b

# Plot the prediction
plot(x = log_length, y = log_mass, type = "l")