GLM: Count models

Introduction
This week we continued to work with the generalized linear model (GLM) and discussed why we might want to use it and how to interpret the results of these tools. The purpose of this lab is to get you comfortable with regression for count data, and help you get comfortable with some of the diagnostics we will use with these tools, while continuing to work with interpreting results with respect to the link functions with which we are working. Next week, we will talk about how we can deal with things like repeated measures on the same categories and nested designs.
By the end of this lab, you should 1) be comfortable specifying generalized linear models for count data in R, 2) be able to apply this tool to analyze count data from start to finish, and 3) be able to diagnose and interpret the results of these models.
We’ll be working with functions from the tidyverse as usual this week so you can go ahead and load that now.
You may choose to complete this assignment using either MLE or Bayesian estimation. If you choose to use MLE, you’ll also need the MASS and car packages. If you choose to use Bayesian, you’ll want to load the rstanarm package for this one!
I am going to load them all so I can do it both ways!
library(tidyverse) # For everything we love
library(MASS) # For negative.binomial family in glm()
library(car) # For Anova()
library(rstanarm)Exercises
Let’s start by reading the file and taking a look at the structure of the data set that we’ll be working with this week.
## year region country sex number
## 1 1986 Africa Senegal Female 15.3
## 2 1987 Africa Mali Female 27.0
## 3 1987 Africa Burundi Female 27.8
## 4 1988 Africa Togo Female 19.7
## 5 1988 Africa Zimbabwe Female 7.2
## 6 1988 Africa Uganda Female 19.1These are data that I downloaded from the World Health Organization’s website free of charge. The data set contains 1099 observations of 5 variables. The variables are year, region, country, sex, and number of individuals per 100 that were underweight. These data are estimates, so they are presented as numeric values. We know that they actually represent counts per some unit (i.e. a rate) so we want to convert them to integer class before we start working with them.
# Now we need to make the counts into an integer because these are
# counts and counts are
uw$number <- as.integer(uw$number)Poisson regression
Start by looking at a single region, we will use Africa in this case.
# Make a new dataframe that contains only those records for which
# the region is `Africa`
africa <-
uw %>%
filter(region == "Africa")Let’s do some data exploration to look at the our sampling distribution of number. Here, a quick histogram of your data should show you what you are looking for.
For thought: Do these data appear to conform to a Poisson distribution?
Now, let’s fit a model using number as the response and take a quick look at some regression diagnostics for the model. We will include the variable sex to see if there are differences between males and females. We will also include the variable year as a numeric variable to determine whether or not there is a linear increase or decrease in the number throughout the time series.
This is basically just ANCOVA, but with a count for y and a different sampling distribution! You can fit the model in MLE using the glm() function like so:
# Fit the model, being sure to specify
# the appropriate error distribution and
# link function.
model <- glm(number ~ year + sex,
data = africa,
family = "negative.binomial"(theta = 1)
)Or, you could fit it using stan_glm() from the rstanarm package like this:
# Fit the model, being sure to specify
# the appropriate error distribution and
# link function.
model <- stan_glm(number ~ year + sex,
data = africa,
family = neg_binomial_2()
)##
## SAMPLING FOR MODEL 'count' NOW (CHAIN 1).
## Chain 1:
## Chain 1: Gradient evaluation took 0.001 seconds
## Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 10 seconds.
## Chain 1: Adjust your expectations accordingly!
## Chain 1:
## Chain 1:
## Chain 1: Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 1: Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 1: Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 1: Iteration: 600 / 2000 [ 30%] (Warmup)
## Chain 1: Iteration: 800 / 2000 [ 40%] (Warmup)
## Chain 1: Iteration: 1000 / 2000 [ 50%] (Warmup)
## Chain 1: Iteration: 1001 / 2000 [ 50%] (Sampling)
## Chain 1: Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 1: Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 1: Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 1: Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 1: Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 1:
## Chain 1: Elapsed Time: 1.313 seconds (Warm-up)
## Chain 1: 1.289 seconds (Sampling)
## Chain 1: 2.602 seconds (Total)
## Chain 1:
##
## SAMPLING FOR MODEL 'count' NOW (CHAIN 2).
## Chain 2:
## Chain 2: Gradient evaluation took 0 seconds
## Chain 2: 1000 transitions using 10 leapfrog steps per transition would take 0 seconds.
## Chain 2: Adjust your expectations accordingly!
## Chain 2:
## Chain 2:
## Chain 2: Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 2: Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 2: Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 2: Iteration: 600 / 2000 [ 30%] (Warmup)
## Chain 2: Iteration: 800 / 2000 [ 40%] (Warmup)
## Chain 2: Iteration: 1000 / 2000 [ 50%] (Warmup)
## Chain 2: Iteration: 1001 / 2000 [ 50%] (Sampling)
## Chain 2: Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 2: Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 2: Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 2: Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 2: Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 2:
## Chain 2: Elapsed Time: 1.406 seconds (Warm-up)
## Chain 2: 1.285 seconds (Sampling)
## Chain 2: 2.691 seconds (Total)
## Chain 2:
##
## SAMPLING FOR MODEL 'count' NOW (CHAIN 3).
## Chain 3:
## Chain 3: Gradient evaluation took 0 seconds
## Chain 3: 1000 transitions using 10 leapfrog steps per transition would take 0 seconds.
## Chain 3: Adjust your expectations accordingly!
## Chain 3:
## Chain 3:
## Chain 3: Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 3: Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 3: Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 3: Iteration: 600 / 2000 [ 30%] (Warmup)
## Chain 3: Iteration: 800 / 2000 [ 40%] (Warmup)
## Chain 3: Iteration: 1000 / 2000 [ 50%] (Warmup)
## Chain 3: Iteration: 1001 / 2000 [ 50%] (Sampling)
## Chain 3: Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 3: Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 3: Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 3: Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 3: Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 3:
## Chain 3: Elapsed Time: 1.288 seconds (Warm-up)
## Chain 3: 1.276 seconds (Sampling)
## Chain 3: 2.564 seconds (Total)
## Chain 3:
##
## SAMPLING FOR MODEL 'count' NOW (CHAIN 4).
## Chain 4:
## Chain 4: Gradient evaluation took 0 seconds
## Chain 4: 1000 transitions using 10 leapfrog steps per transition would take 0 seconds.
## Chain 4: Adjust your expectations accordingly!
## Chain 4:
## Chain 4:
## Chain 4: Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 4: Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 4: Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 4: Iteration: 600 / 2000 [ 30%] (Warmup)
## Chain 4: Iteration: 800 / 2000 [ 40%] (Warmup)
## Chain 4: Iteration: 1000 / 2000 [ 50%] (Warmup)
## Chain 4: Iteration: 1001 / 2000 [ 50%] (Sampling)
## Chain 4: Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 4: Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 4: Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 4: Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 4: Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 4:
## Chain 4: Elapsed Time: 1.346 seconds (Warm-up)
## Chain 4: 1.311 seconds (Sampling)
## Chain 4: 2.657 seconds (Total)
## Chain 4:Before you look at the summary of the model, be sure to have a look at the regression diagnostics for the count model. Does it appear that you have violated the assumptions underlying the model that you have fit? Think about why or why not. This is not a homework question, it is doing the analysis the right way.
Now that you have looked at the regression diagnostics, take a look at the model summary.
##
## Model Info:
## function: stan_glm
## family: neg_binomial_2 [log]
## formula: number ~ year + sex
## algorithm: sampling
## sample: 4000 (posterior sample size)
## priors: see help('prior_summary')
## observations: 378
## predictors: 3
##
## Estimates:
## mean sd 10% 50% 90%
## (Intercept) 36.1 6.3 28.1 36.2 44.2
## year 0.0 0.0 0.0 0.0 0.0
## sexMale 0.1 0.0 0.1 0.1 0.2
## reciprocal_dispersion 7.7 0.8 6.7 7.7 8.7
##
## Fit Diagnostics:
## mean sd 10% 50% 90%
## mean_PPD 20.8 0.6 20.0 20.8 21.6
##
## The mean_ppd is the sample average posterior predictive distribution of the outcome variable (for details see help('summary.stanreg')).
##
## MCMC diagnostics
## mcse Rhat n_eff
## (Intercept) 0.1 1.0 4615
## year 0.0 1.0 4610
## sexMale 0.0 1.0 5533
## reciprocal_dispersion 0.0 1.0 4642
## mean_PPD 0.0 1.0 3884
## log-posterior 0.0 1.0 1627
##
## For each parameter, mcse is Monte Carlo standard error, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence Rhat=1).You’ll note that we have included both categorical and numerical explanatory variables in this model. This makes the interpretation of the model slightly more complicated than some of the simpler models we have looked at so far.
If you try to predict the mean expected value for females (Intercept term) from these coefficients as we have done with previous exercises, we get huge values that don’t make much logical sense. The reason for this is the combination of categorical and numerical explanatory variables. Remember: the interpretation of regression coefficients (or \(Beta_j\)) is the effect of \(X_i\) on \(Y_i\) given that all other \(X\) are held constant. If we simply do:
exp(beta)
…then we are implicitly telling R that the variable year is being held constant at zero. Because the scale of year is large (1986-2015) relative to our counts, we get ridiculously large values if we try to predict the mean value of number forfemale without specifying a reasonable value for year. So, if we want to get a reasonable prediction for the mean expected value of number for females, we need a reasonable value of year. In most cases, unless you are predicting across the range of years, using the mean is fine (although not ideal if it is significant!):
Here is an example of how to predict the mean value for females from the output of the glm() fit above. The process is identical for the estimates from stan_glm() although your estimates will be slightly different.
## [1] 2.950881# Now, we need to use the inverse of
# the link function to get our prediction.
# Since the link function was 'log', we use:
exp(female)## [1] 19.12279We see that the mean number of females per 100 in the African region that were underweight during the time period from 1986 through 2015 was about 19, or 19%. What if we wanted to do this for males? Your turn:
Question 1. What is the mean number of males per 100 in the African region that were underweight during the time period under study? Use the model coefficients to determine this “manually” like I demonstrated above.
Plot the predictions from your model. Note that you may need to combine information from Chapter 13.4 and Chapter 10.4 to accomplish this. Remember: you essentially have a glm() count model that is structured like ANCOVA.
Question 2. Using either your predicted values or the plots you have made, what is the mean difference between males and females during the time period under study? The difference is statistically significant…do you think it is biologically meaningful? Defend your answer.
Negative binomial regression
Now, we will take a step back and start working with the entire data set. Let’s take another quick look at it just to refresh our memories.
## year region country sex number
## 1 1986 Africa Senegal Female 15
## 2 1987 Africa Mali Female 27
## 3 1987 Africa Burundi Female 27
## 4 1988 Africa Togo Female 19
## 5 1988 Africa Zimbabwe Female 7
## 6 1988 Africa Uganda Female 19
## 7 1988 Africa Ghana Female 23
## 8 1990 Africa Nigeria Female 33
## 9 1990 Africa Mauritania Female 42
## 10 1991 Africa United Republic of Tanzania Female 23## [1] Africa Americas Eastern Mediterranean
## [4] Europe South-East Asia Western Pacific
## 6 Levels: Africa Americas Eastern Mediterranean Europe ... Western PacificOkay, so now instead of looking at just one region from the data set, we will look at all six to see if there are differences between regions. Leave us have another exploratory look at the data:
ggplot(uw, aes(x = region, y = number)) +
geom_boxplot(width = .25) +
xlab("Region") +
ylab("Number") +
theme_bw() +
theme(
axis.title.x = element_text(vjust = -1),
axis.title.y = element_text(vjust = 3),
)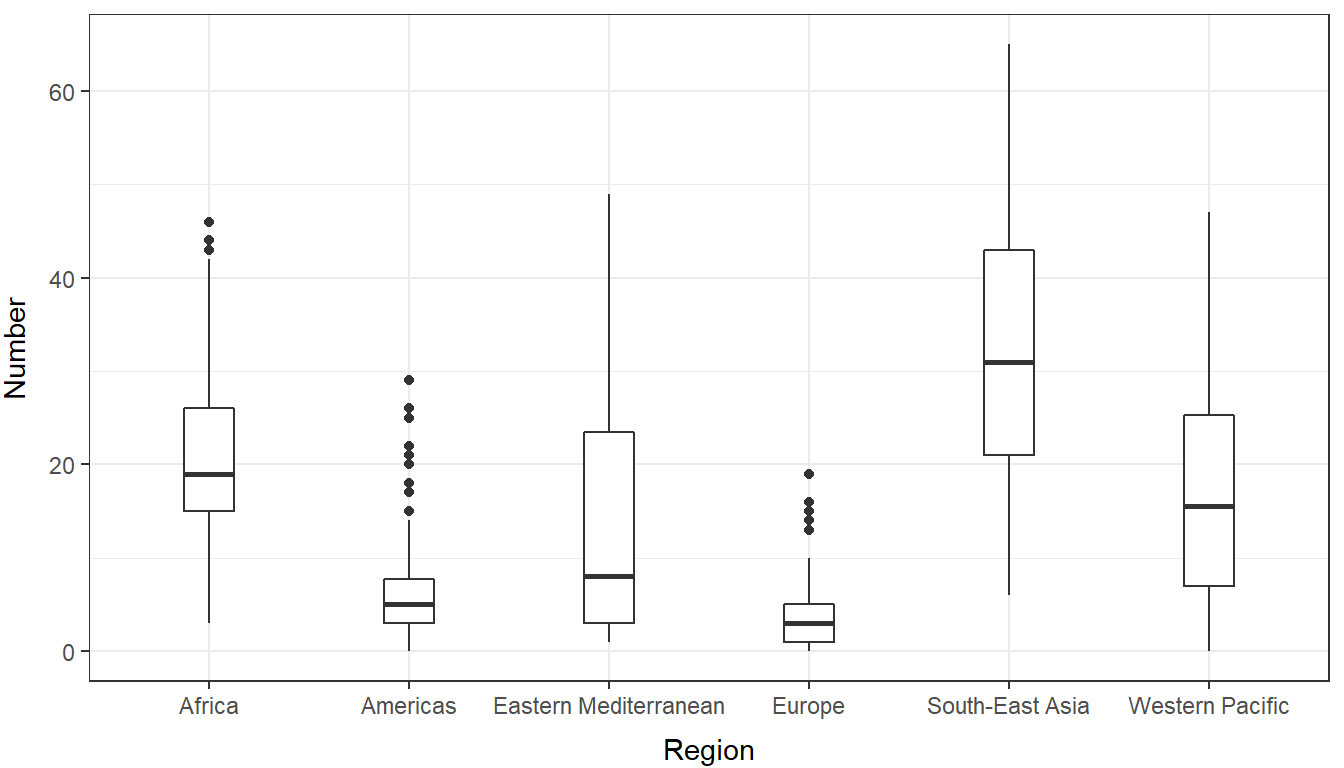
It’s pretty obvious here that no matter which way we slice it, these are decidedly not coming from a Poisson distribution. So, what do we do? This is GLM! We just need to use a different error distribution. From our histogram, it should be clear that we are now working with a negative binomial error structure.
Start by fitting a negative binomial regression model to the data that tests the effect of region (x) on number (y). This one is essentially an ANOVA model, but with counts and a different sampling distribution that we can fit with glm() or stan_glm()!
Here is an example fit with the glm() function:
Here is an example with stan_glm():
##
## SAMPLING FOR MODEL 'count' NOW (CHAIN 1).
## Chain 1:
## Chain 1: Gradient evaluation took 0 seconds
## Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 0 seconds.
## Chain 1: Adjust your expectations accordingly!
## Chain 1:
## Chain 1:
## Chain 1: Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 1: Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 1: Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 1: Iteration: 600 / 2000 [ 30%] (Warmup)
## Chain 1: Iteration: 800 / 2000 [ 40%] (Warmup)
## Chain 1: Iteration: 1000 / 2000 [ 50%] (Warmup)
## Chain 1: Iteration: 1001 / 2000 [ 50%] (Sampling)
## Chain 1: Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 1: Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 1: Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 1: Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 1: Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 1:
## Chain 1: Elapsed Time: 4.26 seconds (Warm-up)
## Chain 1: 3.841 seconds (Sampling)
## Chain 1: 8.101 seconds (Total)
## Chain 1:
##
## SAMPLING FOR MODEL 'count' NOW (CHAIN 2).
## Chain 2:
## Chain 2: Gradient evaluation took 0.001 seconds
## Chain 2: 1000 transitions using 10 leapfrog steps per transition would take 10 seconds.
## Chain 2: Adjust your expectations accordingly!
## Chain 2:
## Chain 2:
## Chain 2: Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 2: Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 2: Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 2: Iteration: 600 / 2000 [ 30%] (Warmup)
## Chain 2: Iteration: 800 / 2000 [ 40%] (Warmup)
## Chain 2: Iteration: 1000 / 2000 [ 50%] (Warmup)
## Chain 2: Iteration: 1001 / 2000 [ 50%] (Sampling)
## Chain 2: Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 2: Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 2: Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 2: Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 2: Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 2:
## Chain 2: Elapsed Time: 4.214 seconds (Warm-up)
## Chain 2: 3.775 seconds (Sampling)
## Chain 2: 7.989 seconds (Total)
## Chain 2:
##
## SAMPLING FOR MODEL 'count' NOW (CHAIN 3).
## Chain 3:
## Chain 3: Gradient evaluation took 0.001 seconds
## Chain 3: 1000 transitions using 10 leapfrog steps per transition would take 10 seconds.
## Chain 3: Adjust your expectations accordingly!
## Chain 3:
## Chain 3:
## Chain 3: Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 3: Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 3: Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 3: Iteration: 600 / 2000 [ 30%] (Warmup)
## Chain 3: Iteration: 800 / 2000 [ 40%] (Warmup)
## Chain 3: Iteration: 1000 / 2000 [ 50%] (Warmup)
## Chain 3: Iteration: 1001 / 2000 [ 50%] (Sampling)
## Chain 3: Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 3: Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 3: Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 3: Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 3: Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 3:
## Chain 3: Elapsed Time: 4.34 seconds (Warm-up)
## Chain 3: 4.044 seconds (Sampling)
## Chain 3: 8.384 seconds (Total)
## Chain 3:
##
## SAMPLING FOR MODEL 'count' NOW (CHAIN 4).
## Chain 4:
## Chain 4: Gradient evaluation took 0 seconds
## Chain 4: 1000 transitions using 10 leapfrog steps per transition would take 0 seconds.
## Chain 4: Adjust your expectations accordingly!
## Chain 4:
## Chain 4:
## Chain 4: Iteration: 1 / 2000 [ 0%] (Warmup)
## Chain 4: Iteration: 200 / 2000 [ 10%] (Warmup)
## Chain 4: Iteration: 400 / 2000 [ 20%] (Warmup)
## Chain 4: Iteration: 600 / 2000 [ 30%] (Warmup)
## Chain 4: Iteration: 800 / 2000 [ 40%] (Warmup)
## Chain 4: Iteration: 1000 / 2000 [ 50%] (Warmup)
## Chain 4: Iteration: 1001 / 2000 [ 50%] (Sampling)
## Chain 4: Iteration: 1200 / 2000 [ 60%] (Sampling)
## Chain 4: Iteration: 1400 / 2000 [ 70%] (Sampling)
## Chain 4: Iteration: 1600 / 2000 [ 80%] (Sampling)
## Chain 4: Iteration: 1800 / 2000 [ 90%] (Sampling)
## Chain 4: Iteration: 2000 / 2000 [100%] (Sampling)
## Chain 4:
## Chain 4: Elapsed Time: 4.171 seconds (Warm-up)
## Chain 4: 4.445 seconds (Sampling)
## Chain 4: 8.616 seconds (Total)
## Chain 4:Plot the residual diagnostics for this model following the approach in Chapter 13.3 or Chapter 18.3 of the textbook. Here is an example of what your plotting code should look like if you’ve followed one of those approaches:
# Get the residuals - will work the same either way!
nb_mod_resids <- data.frame(
uw,
.fitted = nb_mod$fitted.values,
.resid = nb_mod$residuals)
# Plot residuals by Region
ggplot(nb_mod_resids, aes(x = region, y = .resid, fill = region)) +
geom_boxplot(alpha = 0.25, width = 0.25) +
geom_jitter(aes(color = region), width = .1, alpha = 0.1) +
xlab("Fitted values") +
ylab(expression(paste(epsilon)))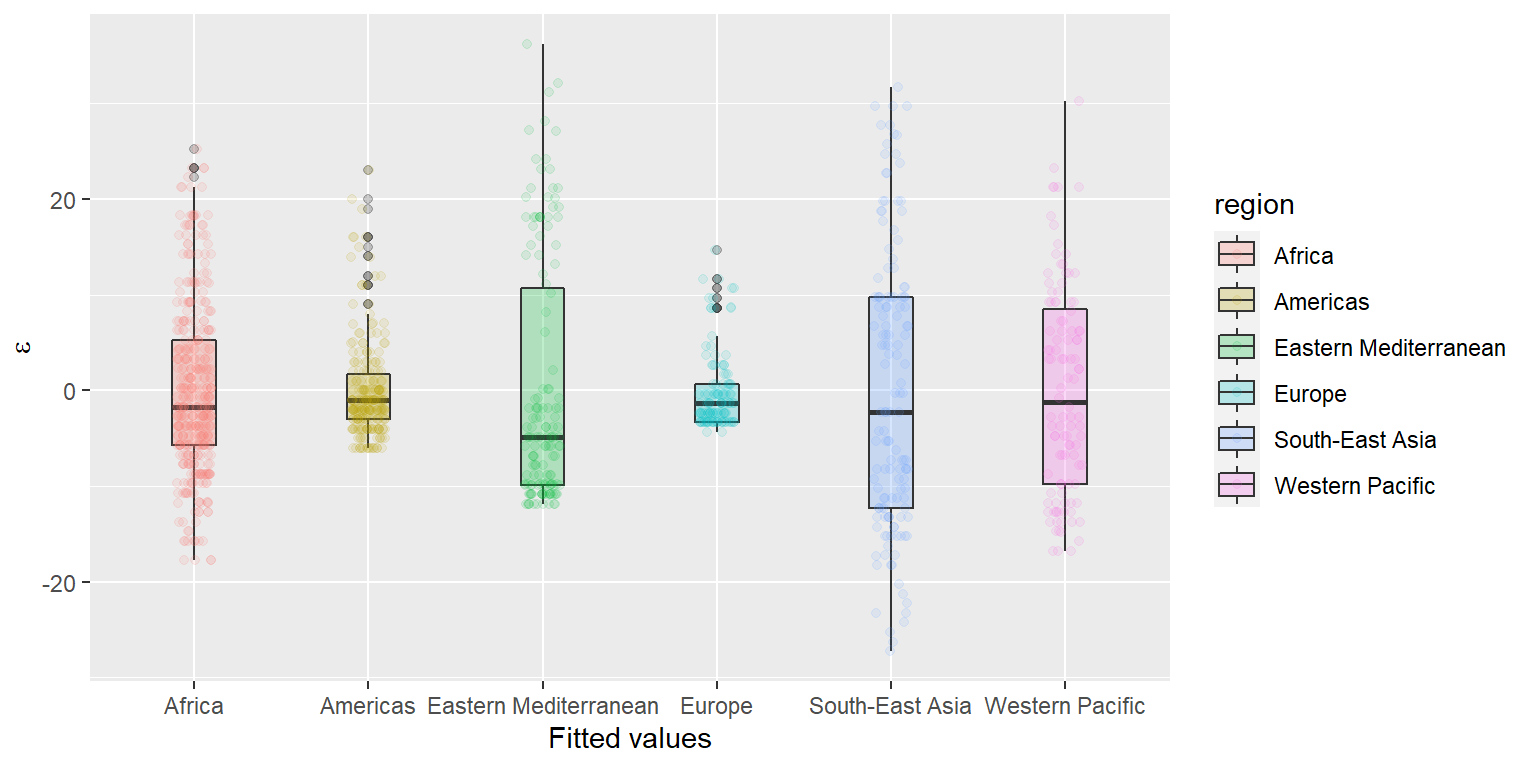
Question 3. Based on the residual diagnostics, does it look like we are in obvious violations of any of our assumptions?
Now that we have done some model validation, let’s have a look at the actual results of our model.
First, check the overall effect of region on number using the Anova() function from the car package if you used the glm() approach:
If you used stan_glm() to fit the model, remember that you’ll want to start by looking at the coefficients. To determine whether any of the regions differ significantly from the intercept:

In either case, we should conclude that there was there a significant effect of region on the number of individuals per 100 that were underweight.
Now, predict the mean number of individuals that were underweight per 100 for each of the regions in this study using the approach demonstrated in Chapter 13.4 or Chapter 18.4.3.
Question 4. Which region reported the greatest number of individuals that were underweight? Which region reported the fewest number of individuals that were underweight?
Now that you have your model results, make a boxplot or violin plot of number by region that shows your predictions over your raw data like we did in Chapter 10.4.1 when we were doing ANOVA (because these are the same things!). Just remember that we need to calculate confidence intervals on the link scale and we’ll need to invert the predictions like we did in Chapter 13 and Chapter 18 (but we don’t have continuous X).
Model selection for count regression
Finally, we can use these data to determine how the number of underweight individuals changed during the time series by region to determine if there were differences in how these numbers changed over time.
Make two models for this section. For the first model, consider only the additive effects of region and year (x variables) on number (y). In the second model, include the interaction effect between region and year on number.
If you fit your models using MLE with the glm() function, use the AIC() function in base R or the aictab() function from AICcmodavg to get the AIC score for each of the two models you have created and compare them to determine whether one of these is “significantly” better than the other. If you used stan_glm() function to fit the models with Bayesian estimation, you can compare the models using LOO-IC or elpdloo from the loo package as we did in Chapters 17 and 18.
Plot the predictions of the best model.
Question 5. According to the AIC scores that you have extracted, is there unequivocal evidence to indicate that one of these models is better than the other? Does this make sense based on your predictive plots given any apparent differences between regions?
This work is licensed under a Creative Commons Attribution 4.0 International License.